最优间隔分类器(Optimal Margin Classifier)。其目标是使得最小几何间隔最大化(10. SVM(一)概念): $$ \text{目标(1):} \\ \max_{w, b} \gamma \\ \text{ s.t. } y^{(i)} \cdot ((\frac{w}{||w||})^T \cdot x^{(i)}+\frac{b}{||w||}) \geq \gamma, i=1,\ldots,n $$ 我们知道,$\hat{\gamma} = \frac{\gamma}{||w||}$,所以上面的目标可以等同于: $$ \text{目标(2):} \\ \max_{w, b} \frac{\hat{\gamma}}{||w||} \\ \text{ s.t. }y^{(i)} \cdot (w^T \cdot x^{(i)}+b) \geq \hat{\gamma}, i=1,\ldots,n $$ 为了最大化上述值,我们有两种策略。
- 增大$\hat{\gamma}$
- 减小$||w||$
针对第一种可能,我们要证明其无效性。假如,我们增大$\hat{\gamma}$到${\hat{\gamma}}_1 := \lambda {\hat{\gamma}}$,因为$\hat{\gamma}=y(w^Tx+b)$,可以视作$w_1:=\lambda w, b_1 = \lambda b$。所以,此时 $$ \frac{\hat{\gamma_1}}{||w_1||}=\frac{\lambda \hat{\gamma}}{||\lambda w||} = \frac{\hat{\gamma}}{||w||} \\ $$ 没有发生任何改变,所以第一条策略不可行。于是,我们可以固定$\hat{\gamma}=1$
此时,上述目标(2)可以表述成: $$ \text{目标(3):} \\ \min_{w, b} \frac{1}{2}||w||^2 \\ \text{ s.t. }y^{(i)} \cdot (w^T \cdot x^{(i)}+b) \geq 1, i=1,\ldots,n $$
因为最小化$||w||$和最小化$\frac{1}{2}||w||^2$是一致的。
拉格朗日乘子法(Lagrange Multiplier)
为了解决上述的凸优化问题,我们引入拉格朗日乘子法Lagrange Multiplier来解决这个问题。
我们首先来看看凸优化问题的定义: $$ \min_wf(w) \\ \text{s.t. }g_i(w) \leq 0, h_i(w) =0 $$ 构建拉格朗日乘子: $$ {\cal L}(w, \alpha, \beta) = f(w)+\sum_i\alpha_ig_i(w)+\sum_i\beta_ih_i(w) $$ 定义: $$ \theta_p(w) = \max_{\alpha_i>0, \beta}{\cal L}(w, \alpha, \beta) $$ 观察$\theta_p(w)$:
- 如果$g_i(w)>0$,那么$\theta_p(w)=+\infty$(因为$\alpha$可以取任意大值)。
- 如果$h_i(w) \neq 0$,那么$\theta_p(w)=+\infty$(因为$\beta$可以取$+\infty/-\infty$)。
所以,在满足约束的情况下,$\theta_p(w)=f(w)$,$\min_w \theta_p(w)=\min_w f(w)$,因为使得${\cal L}(w, \alpha, \beta)$最大的方法,就是其他所有项全是0。那么,可以得出这样的结论: $$ \theta_p(w)=\begin{cases} f(w), &\text{满足约束} \\ \infty, &\text{不满足约束} \end{cases} $$ 因此,在满足条件的情况下,$\min_w\theta_p(w)$等价于$min_wf(w)$。
我们将最优间隔分类器的目标重新表示一下: $$ p^\ast =\min_{w, b}\max_\alpha {\cal L(w, \alpha, b)} \\ {\cal L}(w, \alpha, b) = \frac{1}{2}||w||^2+\sum_i\alpha_i(1-y^{(i)}(w^T x^{(i)}+b)) $$ 其中,直接忽略了$h_i(w)=0$的约束,而$g_i(w,b)=1-y^{(i)}(w^Tx^{(i)}+b) \leq 0, f(w)=\frac{1}{2}||w||^2$
对偶问题(Dual Problem)
一般来说,将原始问题转化成对偶问题来求解。一是因为对偶问题往往比较容易求解,二是因为对偶问题引入了核函数,方便推广到非线性分类的情况。
我们看到,之前的原始问题,是 $$ p^\ast =\min_{w, b}\max_\alpha {\cal L}(w, \alpha, b) $$
那么,定义其对偶问题:
$$ l^\ast =\max_\alpha\min_{w,b}{\cal L}(w, \alpha, b) $$
接下去,我们求解对偶问题:
先求解$\min_{w,b}{\cal L}(w, \alpha, b)$:
分别求偏导,使其等于0,导出最小值: $$ \begin{align} & \nabla_w{\cal L}(w, \alpha, b) =w-\sum_{i=1}\alpha_iy^{(i)}x^{(i)}=0 \\ & \nabla_b{\cal L}(w, \alpha, b) =\sum_{i=1}\alpha_iy^{(i)}=0 \end{align} $$
得到:
$$ w =\sum_{i=1}\alpha_iy^{(i)}x^{(i)} \\ \sum_{i=1}\alpha_iy^{(i)} = 0 $$
代入${\cal L}(w, \alpha, b)$,就可以得到最小值:
$$ \begin{align} {\cal L}(w, \alpha, b) &= \frac{1}{2}||w||^2+\sum_i\alpha_i(1-y^{(i)}(w^T x^{(i)}+b)) \\ \min_{w, b}{\cal L}(w, \alpha, b) &=\underbrace{\sum_{i=1}\alpha_i-\frac{1}{2}\sum_{i=1}\sum_{j=1}\alpha_i\alpha_jy_iy_j(x_i \cdot x_j)}_{W(\alpha)} \end{align} $$
于是,我们的对偶问题简化到了对$W(\alpha)$最大化: $$ \max_\alpha W(\alpha) \\ \text{s.t. }\alpha_i \geq 0, \sum_iy_i\alpha_i=0 $$
假设,我们解得的对偶问题的解为:$\alpha^\ast =[\alpha_1^\ast ,\alpha_2^\ast , \ldots, \alpha_m^\ast ]$,那么最终原始问题的解可以表示成:
$$ w^\ast =\sum_{i=1}\alpha_i^\ast y^{(i)}x^{(i)} $$
在原始问题中,还有$b$未得到解决。我们先来观察一下约束项:
$$
g_i(w,b)=1-y{(i)}(w^Tx^{(i)}+b) \leq 0
$$
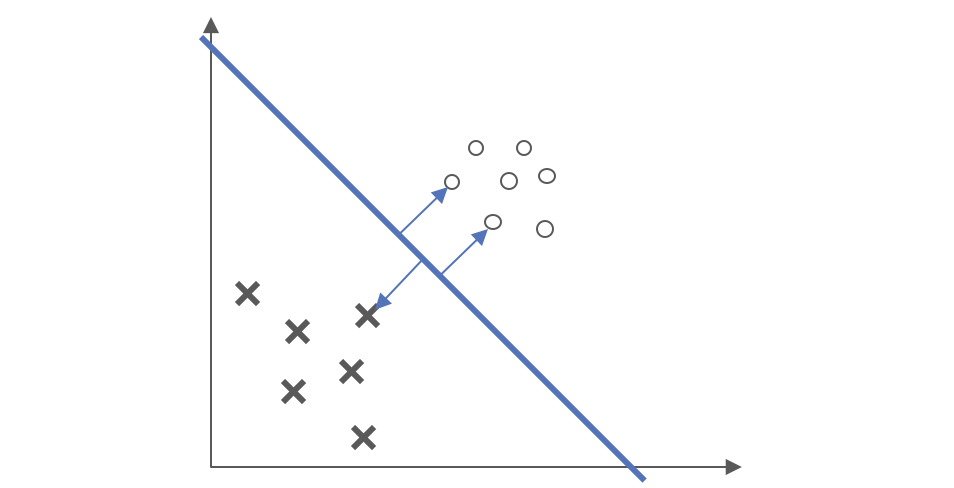
我们知道,在数据中,只有少数的几个数据点,他们的函数距离为1(最小),也即$g_i(w,b)=0$,如图所示。
在整个数据集中,只有这些数据点对约束超平面起了作用,这些数据点被称为支持向量(support vector),其对应的$\alpha_i^\ast \neq 0$,而其他不是支持向量的数据点,没有对约束超平面起作用,其$\alpha_i^\ast =0$。
此时,我们已经得到了$w^\ast $,而$b^\ast $的计算如下,找到一个数据点,其$\alpha_j^\ast \neq 0$(也就是支持向量,其函数间隔为1),我们就能得到:
$$ y^{(j)}(w^{*T}x^{(j)}+b^\ast )=1 \Rightarrow b^\ast =y^{(j)}-\sum_{i=1}\alpha_i^\ast y^{(i)}(x^{(i)} \cdot x^{(j)}) $$